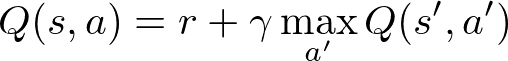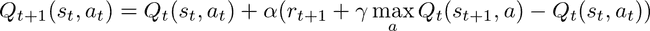Apprentissage par renforcement appliqué au jeu de Poker

Dans cet article, nous présenterons le “Deep Reinforcement Learning”, et plus particulièrement l’algorithme de Deep Q Learning introduit par DeepMind il y a quelques années. Dans une seconde partie, nous implémenterons cet algorithme pour essayer de résoudre certaines situations dans une partie de Poker.

Apprentissage par renforcement

Le Machine Learning ainsi que le Deep Learning sont des sujets très populaires depuis plusieurs années. Grâce aux récentes améliorations apportées au niveau du matériel, notamment des cartes graphiques permettant le calcul parallèle, nous avons assisté ces dernières décennies à d’importantes avancées. Les algorithmes résolvent constamment des tâches très complexes telles que la reconnaissance et la génération d’images / vidéos. Ces algorithmes nécessitent généralement d’énormes jeux de données pour obtenir des performances raisonnables.

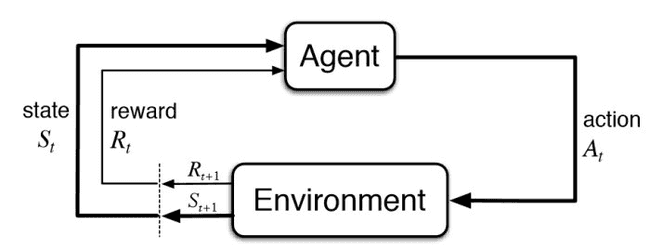
L’apprentissage par renforcement est un type d’apprentissage automatique dans lequel un algorithme n’a pas de données d’entraînement au début. L’objectif est qu’un agent évolue dans un environnement et tire des leçons de sa propre expérience. Pour qu’un algorithme d’apprentissage par renforcement fonctionne, l’environnement dans lequel il évolue doit être calculable et avoir une fonction de récompense qui évalue la qualité d’un agent. C’est pourquoi il peut être facilement appliqué aux jeux, car les états sont clairement définis par le programme, les règles sont généralement simples et il y a un objectif clair (généralement un score permettant de déterminer la qualité de jeu). Cependant, l’apprentissage par renforcement peut également être utilisé pour simuler des problèmes concrets tels que la simulation robotique.

Une représentation du fonctionnement d’un algorithme d’apprentissage par renforcement.

En 2013, la startup DeepMind a publié un article Playing Atari with Deep Reinforcement Learning. Les chercheurs de DeepMind ont réussi à créer un algorithme qui pourrait surpasser les meilleurs joueurs sur de nombreux jeux d’Atari, en utilisant une architecture unique de réseau de neurones artificiels. Cela a été perçu comme le premier pas vers des algorithmes polyvalents. Ils ont introduit des méthodes pour résoudre les problèmes courants rencontrés lors de l’apprentissage par renforcement, qui stagnait depuis plusieurs années déjà.

Q-learning

Q table

L’élément principal de l’algorithme de Q-learning est la table d’état/action. C’est une matrice bidimensionnelle, qui associe un état avec ses valeurs correspondantes Q (s, a) pour chaque action entreprise.

Représentation d’une Q-table, pour 5 états possibles et 5 actions possibles.

L’objectif de l’algorithme est de trouver de manière itérative la Q-table optimale, qui associe les états à leurs valeurs Q(s,a) correctes. Pour cela, nous utilisons l’équation de Bellman :

Cette équation indique que la valeur Q pour un état et une action est égale à la récompense immédiate plus la récompense future actualisée, γ étant le facteur d’actualisation. Notre algorithme essaiera de choisir une action qui maximise cette fonction, en tenant compte des récompenses futures pour l’agent.

A l’aide de l’équation de Bellman, nous pouvons obtenir la fonction de Q-learning, qui nous permet de mettre à jour la Q-table après avoir exécuté une action. Celle-ci inclut un paramètre α qui lui permet de modifier l’influence de chaque mise à jour des valeurs.

L’algorithme de Q-learning se définit donc comme :

Initialiser aléatoirement la Q-table

Répéter jusqu'à ce que la Q-table converge:
  Choisir l'action ( maxQ(s,a) ) depuis la Q-table, en fonction de l'état actuel
  Exécuter l'action
  Mesurer la récompense
  Mettre à jour la Q-table grâce à la fonction de Q-learning

Exploitation vs Exploration

Parce que l’algorithme de Q-learning est un algorithme avide, il choisira toujours l’action qui produit la meilleure valeur Q pour le modèle actuel. Cependant, les différentes valeurs de Q sont générées aléatoirement au début, et l’algorithme peut penser que certaines mauvaises actions obtiennent les récompenses les plus élevées. C’est pourquoi nous devons intégrer un paramètre aléatoire, ce qui obligera l’agent à choisir son action de manière aléatoire un certain pourcentage du temps. Nous pouvons également diminuer cette chance avec le temps pour faire converger l’algorithme vers la fonction optimale Q.

Le but du Q-learning est d’avoir une sorte d’aide-mémoire. Pour chaque état possible, nous calculons la valeur Q de chaque action. L’algorithme peut alors choisir la meilleure action possible pour chaque état de l’environnement.

Cependant, lorsque l’environnement contient de nombreuses dimensions, comme au Poker où il peut y avoir un très grand nombre d’états possibles, le Q-learning devient impraticable. C’est pourquoi Deep Q-Learning a été introduit.

Deep Q-learning

Le Deep Q-Learning est l’algorithme introduit par la publication de DeepMind en 2013. Il s’agit essentiellement d’une extension de l’algorithme de Q-Learning traditionnel qui utilise un réseau de neurones afin d’approximer la valeur de Q(s,a). Cela permet à l’algorithme de s’adapter aux environnements et états complexes, tels que les jeux, comprenant de nombreuses dimensions. Le nombre d’états donnés par l’environnement n’est pas prédéfini.

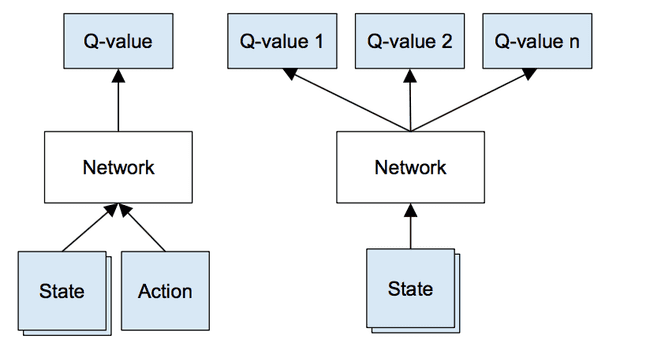
Au lieu d’avoir une matrice Q qui stocke tous les états et actions possibles, nous utilisons un réseau Q, qui est essentiellement un réseau de neurones. Il prend en entrée l’état de l’environnement et fournit la valeur Q prévue pour chaque action.

Le jeu de Poker

Le poker, par opposition au jeu de Go ou aux échecs, est un jeu d’informations incomplètes. Cela signifie que chaque joueur ne connaît qu’une partie de l’état actuel du jeu et que les acteurs doivent déduire certaines de ces informations en fonction des actions des autres.

L’un des aspects complexes du poker est la variance. Parce qu’il repose en partie sur la chance ou plus précisément sur les probabilités, une main favorite à un certain instant peut perdre la partie.

Même après avoir joué des milliers de mains, un joueur ne peut pas être absolument certain que son taux de gain actuel est représentatif de son «vrai» taux de victoire. La seule solution pour atténuer la variance consiste à jouer un très grand nombre de mains qui permettront de faire la moyenne des différentes situations dans le temps. Cependant, il existe des types de jeu où la variance est si élevée que personne ne pourrait jamais avoir une idée du taux de victoire réel. Par exemple, dans les grands tournois, gagner la première place est souvent considéré comme de la loterie.

Grâce à sa relation avec l’argent, le poker est devenu l’un des jeux les plus compétitifs de tous les temps. Depuis le début des salles en ligne, dans les années 2000, le niveau moyen a considérablement augmenté et les meilleurs joueurs prennent dorénavant des décisions presque parfaites. La possibilité de jouer sur des ordinateurs permet aux gens de jouer beaucoup plus rapidement qu’en vrai. L’augmentation du volume par joueur a entraîné de nombreux outils d’analyse. Ces outils, appelés trackers, peuvent enregistrer toutes les mains jouées par un joueur et agréger des statistiques. Cela permet aux gens de trouver leurs propres forces et faiblesses. Ils calculent également des statistiques pour les autres joueurs, ce qui est très utile pour savoir comment exploiter des adversaires sur une table.

Plus récemment, certains outils plus théoriques ont émergé. Ces outils assez onéreux prétendent souvent jouer un jeu parfait. Certains d’entre eux sont commercialisés comme algorithmes d’apprentissage par renforcement, d’autres ne font que bruteforcer (essayer toutes les combinaisons) l’arborescence de chaque situation pour trouver le jeu optimal à chaque situation.

Push-or-fold à deux joueurs

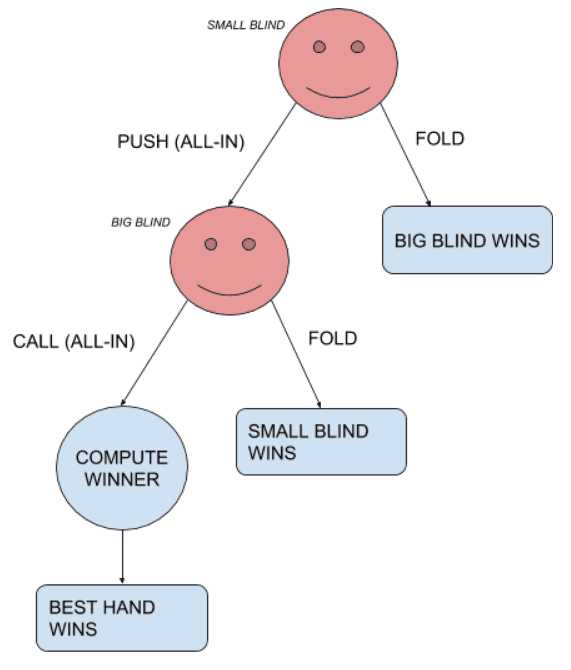
Le jeu de poker a beaucoup de variantes et de types de jeu. L’un des plus simples est le scénario de Push-or-Fold à deux joueurs, dans le Texas Hold’em Poker sans limite. Dans ce scénario, il n’y a que deux joueurs. La Small Blind (premier joueur à agir) n’a que deux actions possibles : se coucher (fold), perdant ainsi la main actuelle, ou se mettre à tapis (push) et risquer tous ses jetons. Une fois que la Small Blind est entrée à tapis, la Big Blind (le deuxième joueur à jouer) a également deux actions possibles : se coucher (fold), ce qui signifie qu’il a perdu la main ou suivre la mise du joueur à tapis. Une fois que les deux joueurs sont all-in, les 5 cartes communes sont distribuées et la meilleure main gagne le pot.

Une représentation de la situation de push-or-fold, avec les différents résultats possibles.

Si aucun jeton n’était impliqué avant de prendre une décision, la stratégie optimale pour cette situation serait que les deux joueurs se couchent toujours et ne jouent à tapis que lorsqu’ils détiennent la meilleure main possible (une paire d’As, une fois toutes les 221 mains distribuées). Cependant, chaque joueur a déjà mis des jetons, les blinds. Si un joueur ne jouait qu’avec les As, il perdrait lentement de l’argent au fil du temps contre un joueur plus agressif. L’idée dans cette situation est de trouver une sorte d’équilibre.

La définition d’un équilibre de Nash est une solution proposée d’un jeu non coopératif impliquant deux joueurs ou plus, dans lequel chaque joueur est supposé connaître les stratégies d’équilibre des autres joueurs. Aucun joueur ne trouvera un intérêt à changer uniquement sa propre stratégie. .

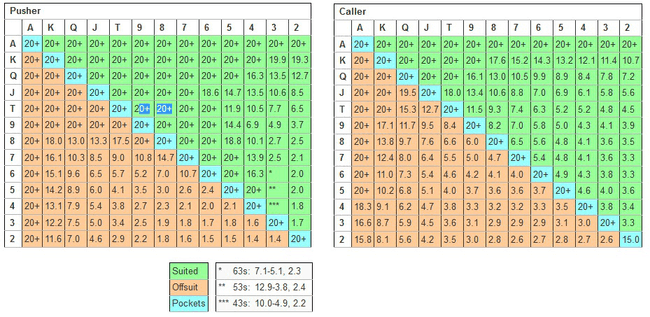
Heureusement, l’équilibre de Nash a déjà été calculé pour ce scénario précis. Ce tableau représente le nombre de jetons nécessaires (en nombre de big blinds) pour que chaque joueur puisse aller à tapis, en fonction de sa main.

Les graphiques optimaux push-or-fold.

Un raisonnement naïf serait que les deux graphiques soient égaux. Cependant, en analysant ceux-ci, nous pouvons voir que la range du Pusher (en Small Blind) est beaucoup plus large que celle du Caller (Big Blind). Dans beaucoup de situations, la Small Blind peut partir à tapis avec un nombre de jetons beaucoup plus large que pour la Big Blind.

Modélisation de l’algorithme

Notre objectif est d’obtenir une approximation de l’équilibre de Nash en utilisant le Deep Q-Learning.

Heureusement, cette situation est très facile, nous pouvons donc grandement simplifier l’algorithme : la récompense sera toujours immédiate, ce qui signifie qu’il n’est pas nécessaire d’implémenter les récompenses futures dans ce scénario, donc pas de facteur de réduction. En utilisant l’équation de Bellman, nous pouvons simplifier l’équation Q-learning : Qt+1(s,a) = Qt(s,a) * α[ r - Qt(s,a) ]

Pour modéliser l’état actuel de la partie, nous encodons 4 caractéristiques :

• La main de départ du joueur
• Si les cartes sont pareillées ou pas
• La position du joueur
• Le nombre de jetons de départ (en Big Blinds)

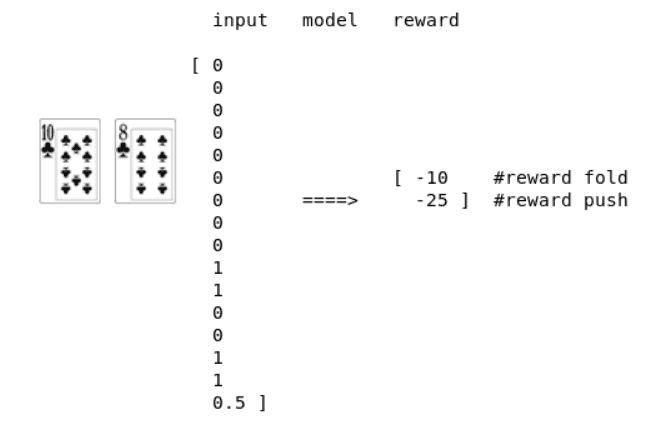
Nous encodons la main de départ en tant que vecteur encodé en one-hot. Le résultat du modèle sera une approximation de la récompense des deux actions possibles (push ou fold).

Une représentation des entrées et des sorties du modèle.

Le modèle utilisé est un simple réseau de neurones connectés multi-couches.

Nous utilisons l’API fonctionnelle Keras pour créer un réseau de neurones à 5 couches :

def preflop_model():

    input_n = Input(shape=(16,), name="input")

    x = Dense(32, activation='relu')(input_n)
    x = Dense(64, activation='relu')(x)
    x = Dense(16, activation='relu')(x)
    out = Dense(2)(x)
    model = Model(inputs=[input_n], outputs=out)
    model.compile(optimizer='adam', loss='mse')

    return model

Pour visualiser notre algorithme, nous entrainons notre réseau avec des milliers d’états aléatoires. Nous déterminons après l’entrainement le seuil de jetons à partir duquel le modèle met tapis ou se couche. Nous mappons ensuite ces valeurs dans une matrice pour obtenir un graphique similaire aux graphiques de référence vus précédemment :

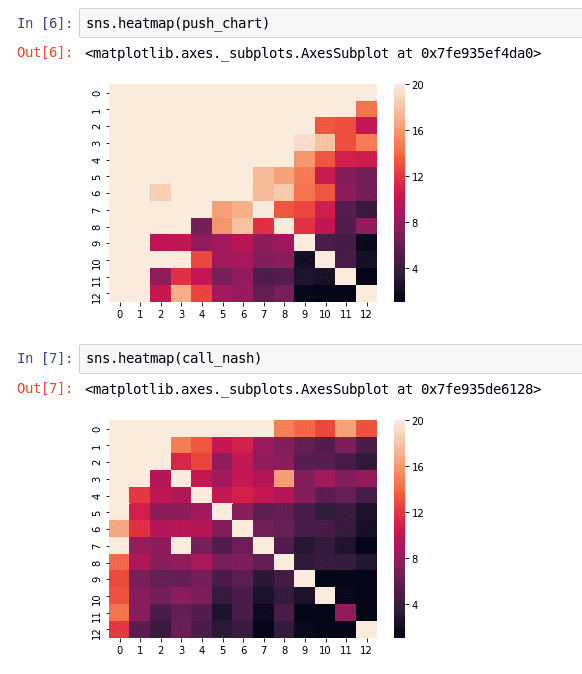
Les range de Push et de Fold données par notre modèle.

Après quelques dizaines de milliers d’itérations, le modèle semble converger. Nous pouvons voir que le modèle a une idée générale de la façon de jouer correctement dans une situation de push ou de fold, le joueur en Small Blind jouant plus large que celui du big blind. Cependant, les résultats sont souvent extrêmes, ce qui signifie que beaucoup de mains iront à tapis quel que soit leur nombre de jeton, tandis que d’autres se coucheront toujours.

Un notebook Jupyter de l’algorithme complet est disponible sur GitHub à cette adresse.

Conclusion

Cette implémentation d’un algorithme de Deep Q-Learning est très simple. Le fait qu’il ne prenne pas en compte les récompenses futures rend l’utilisation de l’algorithme Q-learning moins intéressante, et nous ne pouvons pas encore battre les joueurs du monde réel à aucun jeu de poker. Un deuxième article traitera de la mise en œuvre de cet algorithme sur une main complète de poker, avec davantage de décisions et la mise en œuvre d’outils d’optimisation.

Le code utilisé, ainsi que le moteur de poker conçu pour cette expérimentation, est disponible sur GitHub. Un projet autonome contenant le moteur de jeu (deux joueurs seulement) est disponible à cette adresse.